The test-driven data analysis library, tdda, has two main kinds of functionality

• support for testing complex analytical processes with unittest or pytest
• support for verifying data against constraints, and optionally for discovering such constraints from example data.

Until now, however, the verification process has only reported which constraints failed to be satisfied by a dataset.

We have now extended the tdda library to allow identification of individual failing records, allowing it to act as a general purpose anomaly detection framework.

The new functionality is available through a new detect_df API call, and from the command line with the new tdda detect command.

The diagram shows conceptually how detection works, separating out anomalous records from the rest.

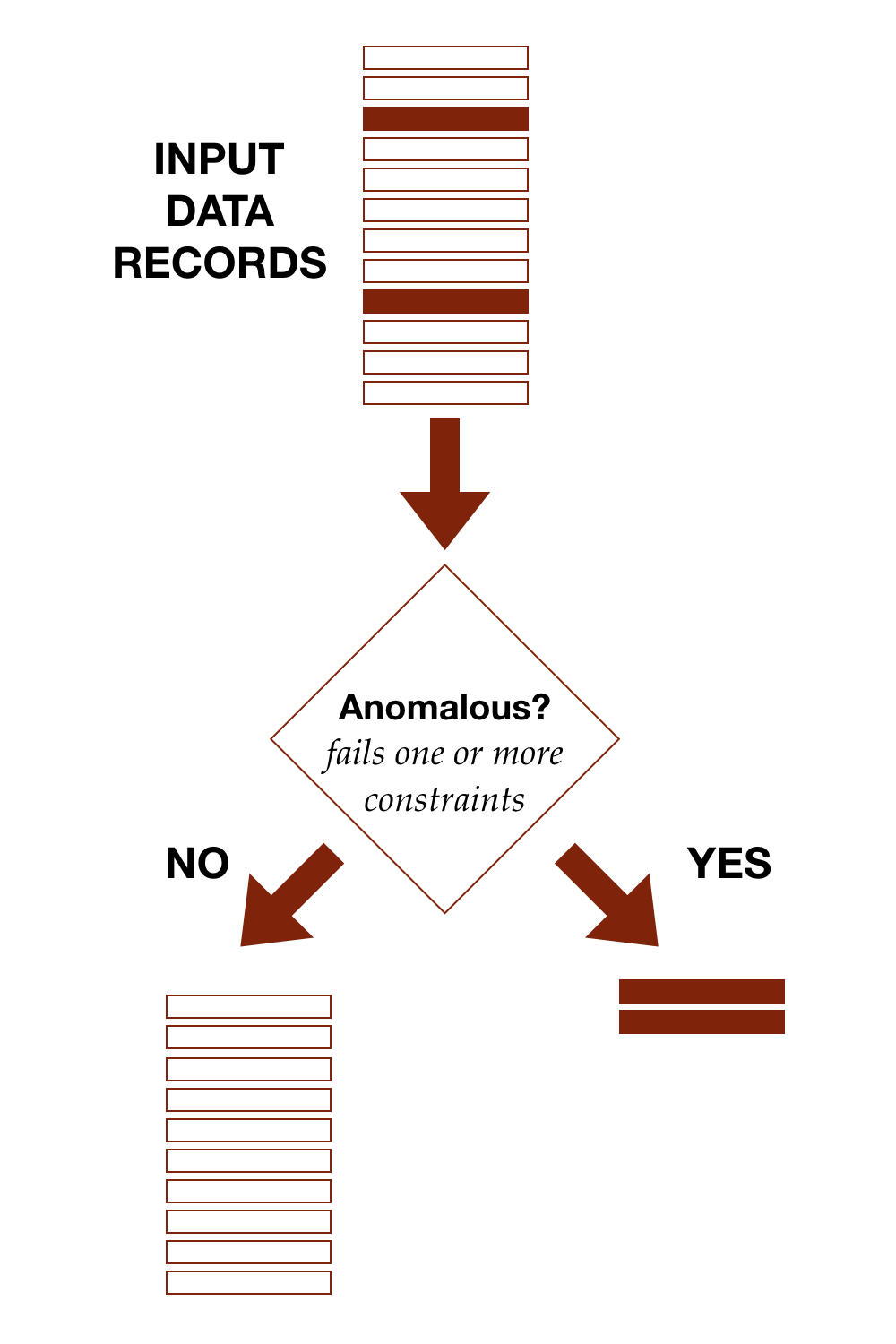
With the TDDA framework, anomalous simply means fails at least one constraint. We'll discuss cases in which the constraints have been developed to try to model some subset of data of interest (defects, high-risk applicants, heart arrythmias, flawless diamonds, model patients etc.) in part II of this post. In those cases, we start to be able to discuss classifications such as true and false positives, and true and false negatives.

Example Usage from the Command Line

Suppose we have a simple transaction stream with just three fields, id, category and price, like this:

       id    category     price
710316821       QT       150.39
516025643       AA       346.69
414345845       QT       205.83
590179892       CB        55.61
117687080       QT       142.03
684803436       AA       152.10
611205703       QT        39.65
399848408       AA       455.67
289394404       AA       102.61
863476710       AA       297.82
534170200       KA        80.96
898969231       QT        81.39
255672456       QT        71.67
133111344       TB       229.19
763476994       CB       338.40
769595502       QT       310.19
464477044       QT        54.41
675155634       QT       199.07
483511995       QT       209.53
416094320       QT        83.31

and the following constraints (which might have been created by hand, or generated using the tdda discover command).

• id (integer): Identifier for item. Should not be null, and should be unique in the table

• category (string): Should be one of “AA”, “CB”, “QT”, “KA” or “TB”

• price (floating point value): unit price in pounds sterling. Should be non-negative and no more than 1,000.00.

This would be represented in a TDDA file with the following constraints.

{
  "fields": {
    "id": {
      "type": "int",
      "max_nulls": 0,
      "no_duplicates": true
    },
    "category": {
      "type": "string",
      "max_nulls": 0,
      "allowed_values":
        ["AA", "CB", "QT", "KA", "TB"]
    },
    "price": {
      "type": "real",
      "min": 0.0,
      "max": 1000.0,
      "max_nulls": 0
    }
  }
}

We can use the tdda verify command to verify a CSV file or a feather file¹ against these files, and get a summary of which constraints pass and fail. If our data is in the file items.feather and the JSON constraints are in constraints.tdda, and there are some violations we will get output exemplified by the following:

$ tdda verify items.feather constraints.tdda
FIELDS:

id: 1 failure  2 passes  type ✓  max_nulls ✓  no_duplicates ✗

category: 1 failure  2 passes  type ✓  max_nulls ✓  allowed_values ✗

price: 2 failures  2 passes  type ✓  min ✓  max ✗  max_nulls ✗

SUMMARY:

Constraints passing: 6
Constraints failing: 4

The new tdda detect command allows us to go further and find which individual records fail.

We can use the following command to write out a CSV file, bads.csv, containing the records that fail constraints:

$ tdda detect items.feather constraints.tdda bads.csv --per-constraint --output-fields

The flag --per-constraint tells the software to write out a boolean column for each constraint, indicating whether the record passed, and the --output-fields tells the software to include all the input fields in the output.

The result is the following CSV file:

id,category,price,id_nodups_ok,category_values_ok,price_max_ok,price_nonnull_ok,n_failures
113791348,TQ,318.63,true,false,true,true,1
102829374,AA,65.24,false,true,true,true,1
720313295,TB,1004.72,true,true,false,true,1
384044032,QT,478.65,false,true,true,true,1
602948968,TB,209.31,false,true,true,true,1
105983384,AA,8.95,false,true,true,true,1
444140832,QT,1132.87,true,true,false,true,1
593548725,AA,282.58,false,true,true,true,1
545398672,QT,1026.4,true,true,false,true,1
759425162,CB,1052.72,true,true,false,true,1
452691252,AA,1028.19,true,true,false,true,1
105983384,QT,242.64,false,true,true,true,1
102829374,KA,71.64,false,true,true,true,1
105983384,AA,10.24,false,true,true,true,1
405321922,QT,85.23,false,true,true,true,1
102829374,,100000.0,false,false,false,true,3
872018391,QT,51.69,false,true,true,true,1
862101984,QT,158.53,false,true,true,true,1
274332319,AA,1069.25,true,true,false,true,1
827919239,QT,1013.0,true,true,false,true,1
105983384,QT,450.68,false,true,true,true,1
102829374,,100000.0,false,false,false,true,3
872018391,QT,199.37,false,true,true,true,1
602948968,KA,558.73,false,true,true,true,1
328073211,CB,1031.67,true,true,false,true,1
405321922,TB,330.97,false,true,true,true,1
334193154,QT,1032.31,true,true,false,true,1
194125540,TB,,true,true,,false,1
724692620,TB,1025.81,true,true,false,true,1
862101984,QT,186.76,false,true,true,true,1
593548725,QT,196.56,false,true,true,true,1
384044032,AA,157.25,false,true,true,true,1

which, we can read a bit more easily if we reformat this (using · to denote nulls) as:

       id  category        price        id  category  price     price  n_failures
                                   _nodups   _values   _max  _nonnull
                                       _ok       _ok    _ok       _ok
113791348        TQ       318.63      true     false   true      true           1
102829374        AA        65.24     false      true   true      true           1
720313295        TB     1,004.72      true      true  false      true           1
384044032        QT       478.65     false      true   true      true           1
602948968        TB       209.31     false      true   true      true           1
105983384        AA         8.95     false      true   true      true           1
444140832        QT     1132.87       true      true  false      true           1
593548725        AA       282.58     false      true   true      true           1
545398672        QT     1,026.40      true      true  false      true           1
759425162        CB     1,052.72      true      true  false      true           1
452691252        AA     1,028.19      true      true  false      true           1
105983384        QT       242.64     false      true   true      true           1
102829374        KA        71.64     false      true   true      true           1
105983384        AA        10.24     false      true   true      true           1
405321922        QT        85.23     false      true   true      true           1
102829374         ·   100,000.00     false     false  false      true           3
872018391        QT        51.69     false      true   true      true           1
862101984        QT       158.53     false      true   true      true           1
274332319        AA     1,069.25      true      true  false      true           1
827919239        QT     1,013.00      true      true  false      true           1
105983384        QT       450.68     false      true   true      true           1
102829374         ·   100,000.00     false     false  false      true           3
872018391        QT       199.37     false      true   true      true           1
602948968        KA       558.73     false      true   true      true           1
328073211        CB     1,031.67      true      true  false      true           1
405321922        TB       330.97     false      true   true      true           1
334193154        QT     1,032.31      true      true  false      true           1
194125540        TB            ·      true      true      ·     false           1
724692620        TB     1,025.81      true      true  false      true           1
862101984        QT       186.76     false      true   true      true           1
593548725        QT       196.56     false      true   true      true           1
384044032        AA       157.25     false      true   true      true           1

Command Line Syntax

The basic form of the command-line command is:

$ tdda detect INPUT CONSTRAINTS OUTPUT

where

• INPUT is normally either a .csv file, in a suitable format, or a .feather file¹ containing a DataFrame, preferably with an accompanying .pmm file¹
• CONSTRAINTS is a JSON file containing constraints, usually with a .tdda suffix. This can be created by the tdda discover command, or edited by hand.
• OUTPUT is again either a .csv or .feather file to be created with the output rows. If the pmmif library is installed, a .pmm metadata file will be generated alongside the .feather file, when .feather output is requested.

Options

Several command line options are available to control the detailed behaviour:

• defaults: If no command-line options are supplied:

  • only failing records will be written
  • only a record identifier and the number of failing constraints will be written.
    • When the input is Pandas, the record identifier will be the index for the failing records;
    • when the input is a CSV file, the record identifier will be the row number, with the first row after the header being numbered 1.

• --per-constraint when this is added, an _ok column will also be written for every constraint that has any failures, with true for rows that satisfy the contraint, false for rows that do not satisfy the constraint and a missing value where the constraint is inapplicable (which does not count as a failure).

• --output-fields [FIELD1 FIELD2 ...] If the --output-fields flag is used without specifying any fields, all fields from the input will be included in the output. Alternatively, a space-separated list of fields may be provided, in which case only those will be included. Whenever this option is used, no index or row-number is written unless specifically requested

• --write-all If this flag is used, all records from the input will be included in the output, including those that have no constraint failures.

• --index This flag forces the writing of the index (for DataFrame inputs) or row number (for CSV inputs).

• --int When writing boolean values to CSV files (either from input data or as per-constraint output fields), use 1 for true and 0 for false.

API Access

The detection functionality is also available through the TDDA library's API with a new detect_df function, which takes similar parameters to the command line. The corresponding call, with a DataFrame df in memory, would be:

from tdda.constraints import detect_df

verification = detect_df(df, 'constraints.tdda', per_constraint=True,
                         output_fields=[])
bads_df = verification.detected()

It is common, when working with tests for analytical processes, for test suites to take non-trivial amount of time to run. It is often helpful to have a convenient way to execute a subset of tests, or even a single test.

We have added a simple mechanism for allowing this to unittest-based tests in the ReferenceTest functionality of the tdda Python library. It is based on tagging tests.

The quick summary is:

• A decorator called tag can be imported and used to decorate individual tests or whole test classes (by preceding the test function or class with @tag).

• When a script calling ReferenceTest.main() is run, if the flag --tagged (or –1, the digit one) is used on the command line, only tagged tests and tests from tagged test classes will be run.

• There is a second new option, --istagged (or –0, the digit zero). When this is used, the software will report only which test classes are tagged, or contain tests that are tagged, and will not actually run any tests. This is helpful if you have a lot of test classes, spread across different files, and want to change the set of tagged tests.

Benefits

The situations where we find this particularly helpful are:

• Fixing a broken test or working on a new feature or dataset. We often find ourselves with a small subset of tests failing (perhaps, a single test case), either because we're adding a new feature, or because something has changed or we are working with data that has slightly different characteristics. If the tests of interest run in a few seconds, but the whole test suite takes minutes or hours to run, we can iterate dramatically faster if we have an easy way to run only the subset of tests currently failing.

• Re-writing test output. The tdda library provides the ability to re-write the expected ("reference") output from tests with whatever the code is currently generating, using the --write-all command-line flag. If it's only a subset of the tests that have failed, there is real benefit in re-writing only the output for the previously failing tests, rather than for all tests. This is particularly true if the reference outputs contain some differences each time (version numbers, dates etc.) that are being ignored using the ignore-lines or ignore-patterns options provided by the library. If we re-write all the tests, and then look at which files have changed, we might see differences in all reference files, whereas if we only regenerate the tests with meaningful changes, we will avoid committing changes that were not required.

Example

We'll illustrate this with a simple example. The code below implements four trivial tests across two classes.

Note the import of the tag decorator function near the top, and that the two of the tests—testTwo and testThree in the class Tests—are decorated with the @tag decorator, as is the entire test class MoreTests.

# tests.py
from tdda.referencetest import ReferenceTestCase, tag

class Tests(ReferenceTestCase):
    def testOne(self):
        self.assertEqual(1, 1)

    @tag
    def testTwo(self):
        self.assertEqual(2, 2)

    @tag
    def testThree(self):
        self.assertEqual(3, 3)

    def testFour(self):
        self.assertEqual(4, 4)


@tag
class MoreTests(ReferenceTestCase):
    def testFive(self):
        self.assertEqual(5, 5)

    def testSix(self):
        self.assertEqual(6, 6)


if __name__ == '__main__':
     ReferenceTestCase.main()

If we run this as normal, all six tests run and pass:

$ python tests.py
......
----------------------------------------------------------------------
Ran 6 tests in 0.000s

OK

But if we add the –1 flag, only four tests run:

$ python tests.py -1
....
----------------------------------------------------------------------
Ran 4 tests in 0.000s

OK

Adding the –v (verbose) flag confirms that these four are the tagged tests, as expected:

$ python tests.py -1 -v
testFive (__main__.MoreTests) ... ok
testSix (__main__.MoreTests) ... ok
testThree (__main__.Tests) ... ok
testTwo (__main__.Tests) ... ok

----------------------------------------------------------------------
Ran 4 tests in 0.000s

OK

Finally, if we want to find out which classes include tagged tests, we can use the –0 flag:

$ python tests.py -0
__main__.MoreTests
__main__.Tests

----------------------------------------------------------------------
Ran 0 tests in 0.000s

OK

This is particularly helpful when our tests are spread across multiple files, as the filenames are then shown as well as the class names.

Installation

Information about installing the library is available in this post.

Other Features

Other features of the ReferenceTest capabilities of the tdda library are described in this post. Its capabilities in the area of constraint discovery and verification are discussed in this post, and this post.

Our previous post introduced the idea of data provenance (a.k.a. data lineage), which has been discussed on a couple of podcasts recently. This is an issue that is close to our hearts at Stochastic Solutions. Here, we'll talk about how we handle this issue, both methodologically and in our Miró software.

We'll focus on seven key ideas from our approach to data provenance:

1. Automatic Logging
2. Audit trail stored in datasets
3. Recording of field definitions and contexts
4. Constraint generation and verification
5. Data Dictionary Generation & Import
6. Data signatures (hashing)
7. Comparing datasets (diff commands)

Automatic Logging

Automatic logging provides a concrete record of all analysis performed in the software.

Our analysis software, Miró, is normally used through a scripting interface that automatically writes several detailed logs. Of these, the most important are:

• A log of all commands executed (in editable, re-executable form)

• A full interleaved log of commands issued and the resulting output, in several forms (including plain text and rich HTML).

Logs build up in a year/month/day/session hierarchy indefinitely, providing a comprehensive (and searchable) record of the analysis that has been performed.

Even when the software is used through the API, the sequence of operations is recorded in the log, though in that case the ability to re-execute the operations is normally lost.

Audit trail

The audit trail in a dataset tracks changes to the data and metadata across sessions, users, and machines, making it possible to see the sequence of operations that led to the current state of the data.

Like a table in a database, or a DataFrame in Pandas or R, Miró's most important data structure is a dataset—a tabular structure with named fields as columns and different observations (records) stored in rows. These form a column-based data store, and datasets can be saved to disk with a .miro extension—a folder that contains the typed data together with rich metadata.

Every time a change is made to a dataset, the operation that caused the change is recorded in the Audit Trail section of the dataset. This is true both for changes to data and to metadata:

• Examples of changes to data in a dataset include creating new fields, deleting fields, filtering out records, appending new records and (more rarely) changing the original values in the data.¹

• Miró maintains many types of metadata, including, field descriptions, field and dataset tags, binnings on fields, long and short names, custom colours and labels, a current record selection (filter) and various formatting information.

In this post, we'll illustrate the most concept using the following small dataset containing transactions for four different customers, identified by id:

Here is the audit trail recorded in that dataset:

In this case, the history is quite short, but includes information about

• where the data originally came from (first line)
• when the data has been saved (second and seventh lines)
• metadata changes (third, fourth and sixth lines)
• changes to the data content (in this case, creation of a new field, days-since-prev).
• detail about when (column 1) and where (column 4) changes were made, in what session these occurred (column 5, linking to the logs), what commands were used (column 3) and where in the log files to find those commands and context (column 6).

Field Definitions and Contexts

Fields remember their definitions, including—where relevant—the context in which they were created. This allows us to understand where any value in a dataset came from, as a sequence of transformations of input values.

In the previous section, we saw that the audit trail contained information about a derived field in the data, including the expression used to derive it. That information is also available as a basic property of the field:

[2]> ls -D days-since-prev
          Field                                 Definition
days-since-prev    (/ (- date (prev-by date id)) 24 60 60)

In other cases, entire datasets are created by taking "measurements" from a base dataset, such as the transactional data shown above. For example, we might want to create a dataset that measures how many transactions each customer has, and their total value.

One way of doing this is Miró is with the following command:

[4]> xtab -d -R MEASURES count sum amount by id
MEASURES: 4 records; 4 (100%) selected; 3 fields.

which creates a new dataset. As you might expect, this is the result:

The field definitions in the dataset created by default) are attached to the fields, as we can see:

[6]> MEASURES.ls -D
    Field                                  Definition
       id             Rollup variable [in trans.miro]
    count         count by id [in dataset trans.miro]
sumamount    sum amount by id [in dataset trans.miro]

Of course, the audit trail for MEASURES also contains this information, together with more detailed information about the session or sessions in which the relevant commands were issued.

Constraint Generation and Verification

Automatically generated constraints can be used to identify anomalous and possibly incorrect data within a source dataset. The can also be used to check that new data with the same structure has similar or expected properties.

We've talked in previous posts (here, here, here, and here) and in a white paper about automatically generating constraints that characterize either all of, or an inferred "good" subset of, the data in a dataset. Such constraints are useful for finding bad and anomalous data in the original dataset, and also for checking ("verifying") new data as it comes in.

We won't go over all the details of constraint generation and verification in this post, but do note that this relates to Roger Peng's idea, discussed in the last post, of tracking changes to data tests as a surrogate for tracking changes to the actual data. Obviously, having generated constraints, it's a good idea to store the constraints under version control, to facilitate such tracking. More directly, the results of verification allow you to see some changes to data directly.

Data Dictionary

The data dictionary provides a useful reference for any user of the data particularly when it includes helpful (and up-to-date) annotations. By making it easily editable, we encourage users to record useful information alongside the data.

Miró can generate a data dictionary from the data. This contains:

• Summary information about the overall dataset

• Per-field information, including

  • basic metadata about each field, including name and type
  • some information about the range of each field, including minimum and maximum values, null count etc.
  • further characterization information, including whether there are duplicate values,
  • any annotations that have been added to the dataset (such as descriptions, alternate names, tags etc.)

Here's an example of the first part of the data dictionary for our transaction dataset:

And here's the second part, with an entry for each field:

While some of the information in the data dictionary is derived directly from the data, other parts (descriptions, alternate names, and tags) are created by annotation actions, whether by humans, bots or scripts. Although there are Miró commands for setting all the (editable) metadata properties, to encourage maximum use, Miró can also export the metadata to a spreadsheet, where users can update it, and then the appropriate parts of the metadata can be re-imported using Miró's importmetadata command.

Data signatures

A data signature is a very compact way to summarize a dataset. This allows quick and efficient checking that analysis is being performed using the correct data.

One of the properties reported in the data dictionary (the first table above) is a hash. If you're not familiar with hashing, a hash function is one that takes a (typically large) input and converts it to a much smaller output. Hash functions are designed so that different inputs tend (but are not guaranteed) to map to different outputs. So if you store the hashes of two large objects and they are different, you can be certain that the objects are different. If the hashes are the same, this does not absolutely guarantee that the objects are the same, but hash functions are designed to make so-called "hash collisions" extremely rare, especially between similar inputs. For most practical purposes, therefore, we can safely assume that if two hashes are the same, the inputs were the same.²

The point of storing the hash is that it acts as a much smaller, very efficient proxy for our original data, and if we want to know whether some dataset we have lying around contains the same data as the one used to generate the data dictionary, all we have to do is compare the hashes.

The hashes that Miró constructs for fields use only the data values, not any metadata, as inputs.³ This is a choice, of course, and we could also hash some or all of the metadata, but our primary concern here is whether we have the same underlying data or not, so we view it as an advantage that the hash is based solely on the data values.

There is an option to store hashes for individual fields, as well, which we have not used in generating the data dictionary shown.

Comparing Datasets (diff commands)

The ability to compare two datasets, and when they are different, to see clearly what the differences are, is as fundamental as the ability to compare two files in Unix or git, or to perform a track changes operation on a Word document.

If we want to compare two datasets to see if they are the same, comparing hashes is a very efficient way to do so.

If, however, we actually want to understand the differences between datasets, we need something more like Unix's diff command, which was discussed in the previous post, or Microsoft Word's Compare Documents functionality.

Miró includes a ddiff command for comparing two datasets. Let's look at an example.

Here's our transaction data again, without the derived days-since-prev field:

and here's a variant of it:

These datasets are small enough that you can probably see the differences by inspection (though it might take a little while to be confident that you've spotted them all), but when there are millions of rows and hundreds of columns, that becomes less easy.

Using the hash trick we talked about previously, we can see whether there are any differences, and slightly more besides. Assuming the current working dataset in Miró is the first, and the second is in TRANS2, we can hash them both:

[46]>  hash
19451c13321284f2b0dd7736b75b443945fac1eae08a8118d600ec0d49b6bf87 id
f3c08f1d2d23abaa06da0529237f63bf8099053b9088328dfd5642d9b06e8f6a date
3a0070ae42b9f341e7e266a18ea1c78c7d8be093cb628c7be06b6175c8b09f23 categ
f5b3f6284f7d510f22df32daac2784597122d5c14b89b5355464ce05f84ce120 amount

b89ae4b74f95187ecc5d49ddd7f45a64849a603539044ae318a06c2dc7292cf9 combined

[47]>  TRANS2.hash
19451c13321284f2b0dd7736b75b443945fac1eae08a8118d600ec0d49b6bf87 id
f3c08f1d2d23abaa06da0529237f63bf8099053b9088328dfd5642d9b06e8f6a date
fcd11dbd69eee0bf6d2a405a6e4ef9227bb3f0279d9cc7866e2efe5b4c97112c categ
64c5c97e9e9676ec085b522303d75ff11b0ebe01a1ceebaf003719b3718f12bb amount

2e171d2a24183e5e25bbcc50d9cd99ad8b4ca48ee7e1abfa6027edd291a22584 combined

We can see immediately that these are different, but that the individual hashes for the id and date fields are the same, indicating that their content is (almost certainly) the same. It's the categ and amount fields that differ between the two datasets.

We can use the ddiff command to get a more detailed diagnosis:

[49]>  ddiff -P TRANS2

Number of differences       Field Pair
           0:                   id : id-2
           0:                 date : date-2
           1:                categ : categ-2
           1:               amount : amount-2

Diff fields:
           1: diff-amount
           1: diff-categ

Total number of differences found: 2

The output here confirms that there are no differences between the id and date fields in the two datasets, but that one value differs for each of the categ and amount fields. The -P flag that we passed to the ddiff command told it to preserve information about the differences, and if we now look at the data, we see five extra fields (on the first dataset)—the fields as they were in the other dataset, TRANS2. Miró also creates an overall diff field showing whether each record has any differences across the two datasets.

[50] show

This makes is easy to identify and select only those fields or records with differences, which is one of the key tasks when trying to track data lineage.

As powerful as Miró's ddiff and related commands are, there is also much more that we would like (and plan) to support. Our comparison is fundamentally based on joining the two datasets (either on one or more nominated key fields, or, as in this case, implicitly on record number). When we are using a join key, it's quite easy to deal with row addition and deletion, but that is harder when we are just joining on record number. It would be useful to have a Unix diff-like ability to spot single rows or groups of rows that have been inserted, deleted, or re-ordered, but we don't have that today. In certain cases, spotting other kinds of systematic edits would be interesting—for example, thinking of the table in speadsheet-like terms, it would be useful to spot cases in which blocks of cells shift up, down, left or right. This situation is not very common in the data we most commonly work with, but there are domains in which those sorts of changes might be frequent.

What Next?

We surveyed a few of the ways we think about and implement features in our software (and workflows) to help track data provenance and data lineage. There's a great deal more we could do, and over time we will almost certainly add more. Hopefully these ideas will prove useful and interesting, and obviously any of you fortunate enough to use Miró can try them out.

We'll keep you posted as we extend our thinking.

Credits

Thanks to our Social Media Manager, for actively policing our content even as it was being created.

In Episode 49 of the Not So Standard Deviations podcast, the final segment (starting at 59:32) discusses data lineage, after Roger Peng listened to the September 3rd (2017) episode of another podcast, Linear Digressions, which discussed that subject.

This is a topic very close to our hearts, and I thought it would be useful to summarize the discussions on both podcasts, as a precursor to writing up how we approach some of these issues at Stochastic Solutions—in our work, in our Miró software and through the TDDA approaches discussed on this blog.

It probably makes sense to begin by summarizing the Linear Digressions, episode, in which Katie Malone explains the ideas of data lineage (also known as data provenance) as the tracking of changes to a dataset.

Any dataset starts from one or more "original sources"—the sensors that first measured the quantities recorded, or the system that generated the original data. In almost all cases, a series of transformations is then applied to the data before it is finally used in some given application. For example, in machine learning, Katie describes typical transformation stages as:

1. Cleaning the data
2. Making additions, subtractions and merges to the dataset
3. Aggregating the data in some way
4. Imputing missing values

She describes this as the process view of data lineage.

An alternative perspective focuses less on the processes than the resulting sequence of datasets, as snapshots. As her co-host, Ben Jaffe points out, this is more akin to the way version control systems view files or collections of files, and diff tools (see below) effectively reconstruct the process view¹ from the data.

In terms of tooling, Katie reckons that the tools for tracking data lineage are relatively well developed (but specialist) in large scientific collaborations such as particle physics (she used to work on the LHC at CERN) and genomics, but her sense is tools are less well developed in many business contexts.

She then describes five reasons to care about data provenance:

1. (To improve/track/ensure) data quality
2. (To provide) an audit trail
3. (To aid) replication (her example was enabling the rebuilding of a predictive model that had been lost if you knew how it had been produced, subject obviously, not only to having the data but full details of the parameters, training regime and any random number seeds used)
4. (To support) attribution (e.g. providing a credit to the original data collector when publishing a paper)
5. Informational, (i.e. to keep track of and aid navigation within large collection of datasets).

I recommend listening to the episode.

In Not-so-Standard Deviations 49, Roger Peng introduces the idea of tracking and versioning data, as a result of listening to Katie and Ben discuss the issue on their podcast. Roger argues that while you can stick a dataset into Git or other version control software, doing so it not terribly helpful because, most of the time the dataset acts essentially as a blob,² rather than as a structured entity that diff tools help you to understand.

In this, he is exactly right. In case you're not familar with version control and diff tools, let me illustrate the point. In a previous post on Rexpy, I added a link to a page about our Miró software between two edits. If I run the relevant git diff command, this is its output:

As you can see, this shows pretty clearly what's changed. Using a visual diff tool, we get an even clearer picture of the changes (especially when the changes are more numerous and complex):

In contrast, if I do a diff on two Excel files stored in Git, I get the following:

git diff b1b85ddc448a723845c36688480cfe5072f28c1a -- test-excel-sheet1.xlsx 
diff --git a/testdata/test-excel-sheet1.xlsx b/testdata/test-excel-sheet1.xlsx
index 0bd63cb..91e5b0e 100644
Binary files a/testdata/test-excel-sheet1.xlsx and b/testdata/test-excel-sheet1.xlsx differ

This is better than nothing, but gives no insight into what has changed. (In fact, it's worse than it looks, because even changes to the metadata inside an Excel file--such as the location of the selected cell—will cause the files to be shown as different. As a result, there are many hard-to-detect false positives when using diff commands with binary files.)

Going back to the podcast, Hilary Parker then talked about the difficulty of the idea of data provenance in the context of streaming data, but argued there was a bit more hope with batch processes, since at least the datasets used then are "frozen".

Roger then argued that there are good custom tools used in particular places like CERN, but those are not tools he can just pick up and use. He then wondered aloud whether such tools cannot really exist, because they require too much understanding on analytical goals. (I don't agree with this, as the next post will show.) He then rowed back slightly, saying that maybe it's too hard for general data, but more reasonable in a narrower context such as "tidy data".

If you aren't familiar with the term "tidy data", it really just refers to data stored in the same way that relational databases store data in tables, with columns corresponding to variables, rows corresponding to whatever the items being measured are (the observations), consistent types for all the values in a column and a resulting regular, grid-like structure. (This contrasts with, say, JSON data, which is hierarchical, and with many spreadsheets, in which different parts of the sheet are used for different things, and with data in which different observations are in columns and the different variables are in rows.) So "tidy data" is an extremely large subset of the data we use in structured data analysis, at least after initial regularization.

Hilary then mentioned an R package called testdat, that she had had worked on at an "unconference". This aimed to test things check things like missing values and contiguity of dates in datasets. These ideas are very similar to those of constraint generation and verification, which we frequently discuss on this blog, as supported in the TDDA package. But Hilary (and others?) concluded that the package was not really useful, and that what was more important was tools to make writing tests for data easier. (I guess we disagree that general tools like this aren't useful, but very much support the latter point.)

Roger then raised the idea of tracking changes to such tests as a kind of proxy for tracking changes to the data, though clearly this is a very partial solution.

Both podcasts are interesting and worth a listen, but both of them seemed to feel that there is very little standardization in this area, and that it's really hard.

We have a lot of processes, software and ideas addressing many aspects of these issues, and I'll discuss them and try to relate them to the various points raised here in a subsequent post, fairly soon, I hope.

We have a new White Paper available:

Automatic Constraint Generation and Verification

Abstract

Correctness is a key problem at every stage of data science projects: completing an entire analysis without a serious error at some stage is surprisingly hard. Even errors that reverse or completely invalidate the analysis can be hard to detect. Test-Driven Data Analysis (TDDA) attempts to identify, reduce, and aid correction of such errors. A core tool that we use in TDDA is Automatic Constraint Discovery and Verification, the focus of this paper.

Download White Paper here