Consistency Checking of Inputs, Outputs and Intermediates
While the idea of regression
testing comes
straight from test-driven
development,
the next idea we want to discuss is associated more with general
defensive
progamming than
TDD. The idea is consistency checking, i.e. verifying that
what might otherwise be implicit assumptions are in fact met by adding
checks at various points in the process.
Initially, we will assume that we are working with tabular data,
but the ideas can be extended to other kinds of data.
Inputs. It is useful to perform some basic checks on inputs.
Typical things to consider include:
-
Are the names and types fields in the input data as we expect?
In most cases, we also expect field names to be distinct,
and perhaps to conform to some rules.
-
Is the distribution of values in the fields reasonable? For example,
are the minimum and maximum values reasonable?
-
Are there nulls (missing values) in the data, and if so, are they
permitted where they occur? If so, are there any restrictions
(e.g. may all the value for a field or record be null?)
-
Is the volume of data reasonable (exactly as expected, if there is
a specific size expectation, or plausible, if the volume is variable)?
-
Is any required metadata included?
In addition to basic sense checks like these, we can also often
formulate self-consistency checks on the data.
For example:
-
Are any of the fields identifiers or keys for which every value should
occur only once?
-
Are there row-level identities that should be true? For example, we
might have a set of category counts and an overall total, and
expect the category totals to sum to the overall total:
nCategoryA + nCategoryB + nCategoryC = nOverall
-
For categorical data, are all the values found in the data allowed,
and are any required values missing?
-
If the data has a time structure, are the times and dates
self-consistent? For example, do any end dates precede start dates?
Are there impossible future dates?
-
Are there any ordering constraints on the data, and if so are they
respected?
Our goal in formulating TDDA is pragmatic: we are not suggesting it is
necessary to check for every possible inconsistency in the input
data. Rather, we propose that even one or two simple, well-chosen
checks can catch a surprising number of problems. As with regression
testing, an excellent time to add new checks is when you discover
problems. If you add a consistency check every time you discover bad
inputs that such a test would have caught, you might quickly build up
a powerful, well-targeted set of diagnostics and verification
procedures. As we will see below, there is also a definite
possibility of tool support in this area.
Intermediate Results and Outputs. Checking intermediates and
outputs is very similar to checking inputs, and all same kinds of
tests can be applied. Some further questions to consider in these
contexts include:
-
If we look up reference data, do (and should) all the lookups succeed?
And are failed lookups handled appropriately?
-
If we calculate a set of results that should exhibit some identity
properties, do those hold? Just as physics has
conservation laws for quantities such as energy and momentum,
there are similar conservation principles in some analytical calculations.
As a simple example, if we categorize spending into different,
non-overlapping categories, the sum of the category totals should
usually equal the sum of all the transactions, as long as we are
careful about things like non-categorized values.
-
If we build predictive models, do they cross-validate correctly
(if we split the data into a training subset and a validation subset)?
And, ideally, do they also validate longitudinally (i.e., on later data,
if this is available)?
Transfer checks. With data analysis, our inputs are frequently generated
by some other system or systems. Often those systems
already perform some checking or reporting of the data they
produce. If any information about checks or statistics from source
systems is available, it is useful to verify that equivalent
statistics calculated over the input data produce the same
results. If our input data is transactional, maybe the source system
reports (or can report) the number or value of transactions over some
time period. Perhaps it breaks things down by category. Maybe we know
other summary statistics or there are checksums available that can
be verified.
The value of checking that the data received is the same as the data
the source system was supposed to send is self-evident, and can help
us to detect a variety of problems including data loss, data
duplication, data corruption, encoding issues, truncation errors and
conversion errors, to name but a few.
Tool Support: Automatic constraint suggestion
A perennial obstacle to better testing is the perception that it is a
"nice to have", rather than a sine qua non, and that implementing it
will require much tedious work. Because of this, any automated support
that tools could provide would seem to be especially
valuable.
Fortunately, there is low-hanging fruit in many areas, and one of
of our goals with this blog is to explore various tool enhancements.
We will do this first in our own Miró software and then, as we find
things that work, will try to produce some examples, libraries and
tools for broader use, probably focused around the Python data
analysis stack.
In the spirit of starting simply, we're first going to look at what
might be possible by way of automatic input checking.
One characteristic of data analysis is that we often start by trying
to get a result from some particular dataset, rather than
setting out to implement an analytical process to be used
repeatedly with different inputs.
In fact, when we start, we may not even have a very specific
analytical goal in mind: we may simply have some data (perhaps
poorly documented) and perform exploratory analysis with some broad
analytical goal in mind. Perhaps we will stop when we have a result
that seems useful, and which we have convinced ourselves is plausible.
At some later point, we may get a similar dataset (possibly pertaining
to a later period, or a different entity) and need to perform a similar
analysis. It's at this point we may go back to see whether we can
re-use our previous, embryonic analytical process, in whatever form
it was recorded.
Let's assume, for simplicity, that the process at least exists as some
kind of executable script, but that it's "hard-wired" to the previous
data. We then have three main choices.
-
Edit the script (in place) to make it work with the new input data.
-
Take a copy of the script and make that work with the new input data.
-
Modify the script to allow it to work with either the new or the old
data, by parameterizing and generalizing it.
Presented like this, the last sounds like the only sensible approach,
and in general it is the better way forward. However, we've all taken the
other paths from time to time, often because under pressure just changing
a few old hard-wired values to new hard-wired values seems as if it
will get us to our immediate result faster.
The problem is that even if were very diligent when preparing the first
script, in the context of the original analysis, it is easy for there
to be subtle differences in a later dataset that might compromise or
invalidate the analysis, and it's hard to force ourselves to be as
vigilent the second (third, fourth, ...) time around.
A simple thing that can help is to generate statements about the original
dataset and record these as constraints. If a later dataset violates
these constraints, it doesn't necessarily mean that anything is wrong,
but being alerted to the difference at least offers us an opportunity
to consider whether this difference might be significant or problematical,
and indeed, whether it might indicate a problem with the data.
Concretely: let's think about what we probably know about a dataset
whenever we work with it. We'll use the Periodic Table as an example
dataset, based on a snapshot of data I extracted from Wikipedia a few
years ago. This is how Miró summarizes the dataset if we ask for a
"long" listing of the fields with its ls -l command:
Field Type Min Max Nulls
Z int 1 92 0
Name string Actinium Zirconium 0
Symbol string Ac Zr 0
Period int 1 7 0
Group int 1 18 18
ChemicalSeries string Actinoid Transition metal 0
AtomicWeight real 1.01 238.03 0
Etymology string Ceres zircon 0
RelativeAtomicMass real 1.01 238.03 0
MeltingPointC real -258.98 3,675.00 1
MeltingPointKelvin real 14.20 3,948.00 1
BoilingPointC real -268.93 5,596.00 0
BoilingPointF real -452.07 10,105.00 0
Density real 0.00 22.61 0
Description string 0.2 transition metal 40
Colour string a soft silver-white ... yellowish green or g ... 59
For each field, we have a name, a type, minimum and maximum values and
a count of the number of missing values. [Scroll sideways if your
window is too narrow to see the Nulls column on the right.] We also
have, implicitly, the field order.
This immediately suggests a set of constraints we might want to construct.
We've added an experimental command to Miró for generating constraints based
on the field metadata shown earlier and a few other statistics.
First, here's the "human-friendly" view that Miró produces if we use
its autoconstraints -l command.
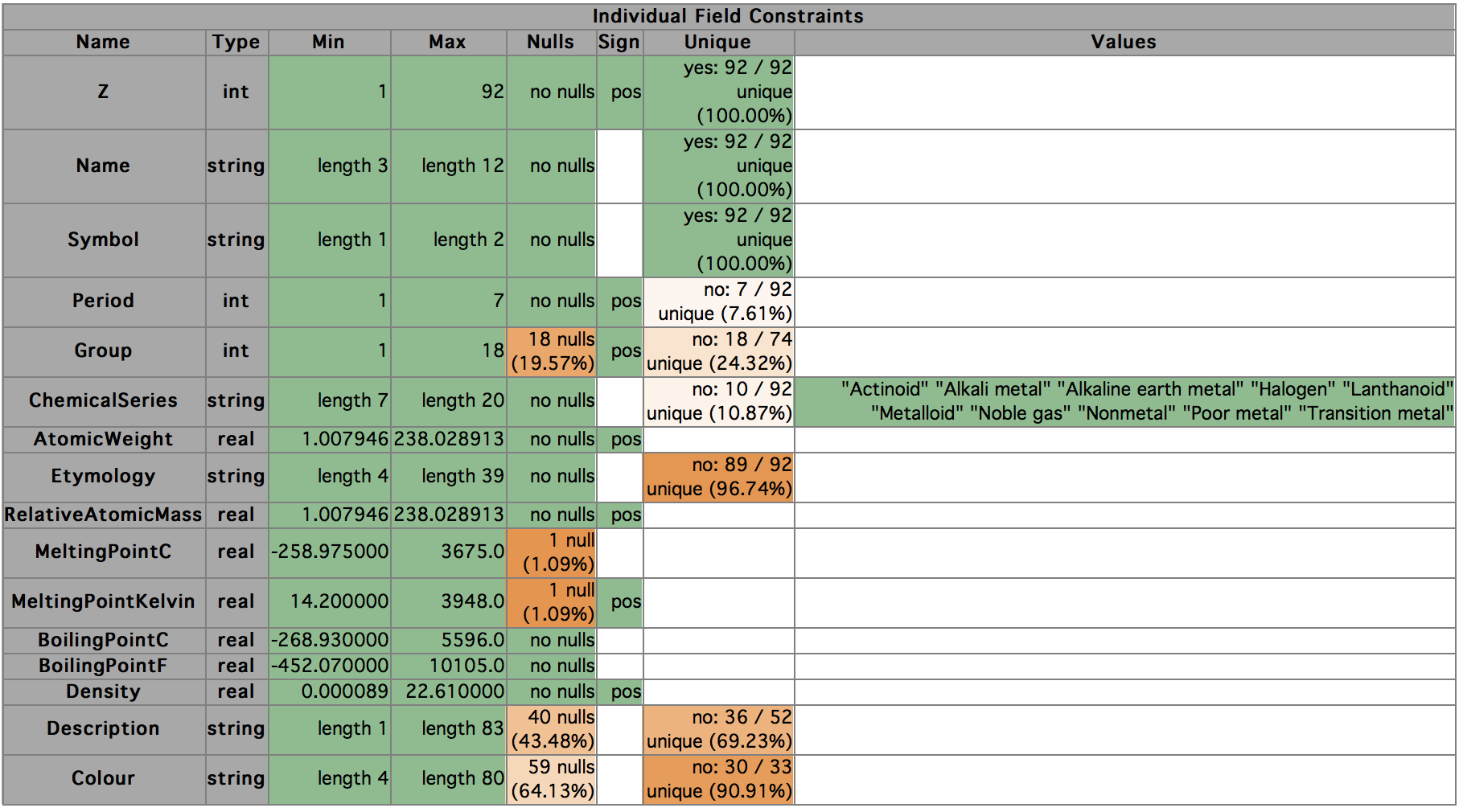
In this table, the green cells represent constraints the system
suggests for fields, and the orange cells show areas in which
potential constraints were not constructed, though they would have
been had the data been different. Darker shades of orange indicate
constraints that were closer to be met within the data.
In addition to this human-friendly view, Miró generates out a set of
declarations, which can be thought of as candidate assertions.
Specifically, they are statements that are true in the current
dataset, and therefore constitute potential checks we might want to
carry out on any future input datasets we are using for the same
analytical process.
Here they are:
declare (>= (min Z) 1)
declare (<= (max Z) 92)
declare (= (countnull Z) 0)
declare (non-nulls-unique Z)
declare (>= (min (length Name)) 3)
declare (<= (min (length Name)) 12)
declare (= (countnull Name) 0)
declare (non-nulls-unique Name)
declare (>= (min (length Symbol)) 1)
declare (<= (min (length Symbol)) 2)
declare (= (countnull Symbol) 0)
declare (non-nulls-unique Symbol)
declare (>= (min Period) 1)
declare (<= (max Period) 7)
declare (= (countnull Period) 0)
declare (>= (min Group) 1)
declare (<= (max Group) 18)
declare (>= (min (length ChemicalSeries)) 7)
declare (<= (min (length ChemicalSeries)) 20)
declare (= (countnull ChemicalSeries) 0)
declare (= (countzero
(or (isnull ChemicalSeries)
(in ChemicalSeries (list "Actinoid" "Alkali metal"
"Alkaline earth metal"
"Halogen" "Lanthanoid"
"Metalloid" "Noble gas"
"Nonmetal" "Poor metal"
"Transition metal"))))
0)
declare (>= (min AtomicWeight) 1.007946)
declare (<= (max AtomicWeight) 238.028914)
declare (= (countnull AtomicWeight) 0)
declare (> (min AtomicWeight) 0)
declare (>= (min (length Etymology)) 4)
declare (<= (min (length Etymology)) 39)
declare (= (countnull Etymology) 0)
declare (>= (min RelativeAtomicMass) 1.007946)
declare (<= (max RelativeAtomicMass) 238.028914)
declare (= (countnull RelativeAtomicMass) 0)
declare (> (min RelativeAtomicMass) 0)
declare (>= (min MeltingPointC) -258.975000)
declare (<= (max MeltingPointC) 3675.0)
declare (>= (min MeltingPointKelvin) 14.200000)
declare (<= (max MeltingPointKelvin) 3948.0)
declare (> (min MeltingPointKelvin) 0)
declare (>= (min BoilingPointC) -268.930000)
declare (<= (max BoilingPointC) 5596.0)
declare (= (countnull BoilingPointC) 0)
declare (>= (min BoilingPointF) -452.070000)
declare (<= (max BoilingPointF) 10105.0)
declare (= (countnull BoilingPointF) 0)
declare (>= (min Density) 0.000089)
declare (<= (max Density) 22.610001)
declare (= (countnull Density) 0)
declare (> (min Density) 0)
declare (>= (min (length Description)) 1)
declare (<= (min (length Description)) 83)
declare (>= (min (length Colour)) 4)
declare (<= (min (length Colour)) 80)
Each green entry in the table maps to a declaration in this list.
Let's look at a few:
-
Min and Max. Z is the atomic number. Each element has an atomic
number, which is the number of protons in the nucleus, and each is unique.
Hydrogen has the smallest number of
protons, 1, and in this dataset, Uranium has the largest number—92.
So the first suggested constraints are that these values
should be in the observed range. These show up as the first two
declarations:
declare (>= (min Z) 1)
declare (<= (max Z) 92)
We should say a word about how these constraints are expressed.
Miró includes expression language called (lisp-like),
(because it's essentially a dialect of
Lisp).
Lisp is slightly unusual in that instead of writing f(x, y) you
write (f x y). So the first expression would be more commonly
expressed as
in regular ("infix")
languages.
Lisp weirdness aside, are these sensible constraints? Well, the first
certainly is. Even if we find some elements beyond Uranium (which we will,
below), we certainly don't expect them to have zero or negative numbers
of protons, so the first constraint seems like a keeper.
The second constraint is much less sensible. In fact, given that
we know the dataset includes every value of Z from 1 to 92, we
confidently expect that any future revisions of the periodic table
will include values higher than 92. So we would probably discard
that constraint.
The crucial point is that no one wants to sit down and write out
a bunch of constraints by hand (and anyway, "why have a dog an
bark yourself?"). People are generally much more willing to review
a list of suggested constraints and delete the ones that don't
make sense, or modify them so that they do.
-
Nulls. The next observation about Z is that it contains no nulls.
This turns into the (lisp-like) constraint:
declare (= (countnull Z) 0)
This is also almost certainly a keeper: we'd probably be pretty unhappy
if we received a Periodic Table with missing Z values for any elements.
(Here, (countnull Z) just counts the number of nulls in field Z,
and = tests for equality, so the expression reads "the number of nulls
in Z is equal to zero".)
-
Sign. The sign column is more interesting.
Here, we have recorded the fact that all the values in Z are positive.
Clearly, this is a logically implied by the fact that the minimum
value for Z is 1, but we think it's useful to record two separate
observations about the field—first, that its minimum value is 1,
and secondly that it is always strictly positive. In cases where the
minimum is 1, for an integer field, these statements are entirely
equivalent, but if the minimum had been (say) 3, they would be different.
The value of recording these observations separately arises if at some
later stage the minimum changes, while remaining positive. In that case,
we might want to discard the specific minimum constraint, but leave
in place the constraint on the sign.
Although we record the sign as a separate constraint in the table,
in this case it does not generate a separate declaration, as it would
be identical to the constraint on the minimum that we already have.
In contrast, AtomicWeight, has a minimum value around 1.008, so it
does get a separate sign constraint:
declare (> (min AtomicWeight) 0)
-
Uniqueness of Values. The next thing our autoconstraints
framework has noticed about Z is that none of its values is
repeated in the data—that all are unique (a.k.a. distinct).
The table reports this as yes (the values are unique) and 92/92
(100%), meaning that there are 92 distinct values and 92 non-null
values in total, so that 100% of values are unique. Other fields,
such as Etymology, have potential constraints that are not quite
met: Etymology has 89 different values in the field, so the ratio of
distinct values to values is about 97%.
NOTE: in considering this, we ignore nulls if there are
any. You can see this if you look at the Unique entry for the
field Group: here there are 18 different (non-null) values for
Group, and 74 records have non-null values for Group.
There is a dedicated function in (lisp-like) for checking whether
the non-null values in a field are all distinct, so the expression
in the declaration is just:
which evaluates to true or false.
-
Min and Max for String Fields.
For string fields, the actual minimum and maximum values are
usually less interesting. (Indeed, there are lots of reasonable
alternative sort orders for strings, given choices such as case
sensitivity, whether embedded numbers should be sorted numerically
or alphanumerically, how spaces and punctuation should be handled,
what to do with accents etc.) In the initial implementation,
instead of using any min and max string values as the basis of
constraints, we suggest constraints based on string length.
For the string fields here, none of the constraints is
particularly compelling, though a minimum length of 1 might be
interesting and you might even think that a maximum length of 2 is
sensible the symbol is useful. But in many cases they will be.
One common case is fixed-length strings, such as the increasingly
ubiquitous UUIDs,
where the minimum and maximum values would both 36 if they are
canonically formatted. (Of course, we can add much stronger
constraints if we know all the strings in a field are UUIDs.)
-
Categorical Values.
The last kind of automatically generated constraint we will
discuss today is a restriction of the values in a field to be
chosen from some fixed set. In this case, Miró has noticed that
there are only 10 different non-null values for ChemicalSeries, so
has suggested a constraint to capture that reality. The slightly
verbose way this currently gets expressed as a constraint is:
declare (= (countzero
(or (isnull ChemicalSeries)
(in ChemicalSeries
(list "Actinoid" "Alkali metal"
"Alkaline earth metal"
"Halogen" "Lanthanoid" "Metalloid" "Noble gas"
"Nonmetal" "Poor metal" "Transition metal"))))
0)
(The or statement starting on the second line is true for field
values that are either in the list or null. The countzero
function, when applied to booleans, counts false values, so this
is saying that none of the results of the or statement should be false,
i.e. all values should be null or in the list. This
would be more elegantly expressed with an (all ...) statement;
we will probably change it to that formulation soon, though the
current version is more useful for reporting failures.)
The current implementation generates these constraints only when
the number of distinct values it sees is 20 or fewer, only for
string fields, and only when not all the values in the field are
distinct, but all of these aspect can probably be improved, and
the user can override the number of categories to allow.
In addition to these constraints, we should also probably generate
constraints on the field types and, as we will discuss in future
articles, dataset-level constraints.
Tool Support: Using the Declarations
Obviously, if we run test the constraints against the same dataset
we used to generate them, all the constraints should be (and are!)
satisfied. Things are slightly more interesting if we run them
against a different dataset.
In this case, we excluded transuranic elements from the dataset
we used to generate the constraints. But we can add them in.
If we do so, and then execute a script (e92.miros) containing
the autogenerated constraints, we get the following output:
$ miro
This is Miro, version 2.1.90.
Copyright © Stochastic Solutions 2008-2015.
Seed: 1463187505
Logs started at 2015/11/25 17:08:23 host tdda.local.
Logging to /Users/njr/miro/log/2015/11/25/session259.
[1]> load elements
elements.miro: 118 records; 118 (100%) selected; 16 fields.
[2]> . e92
[3]> # Autoconstraints for dataset elements92.miro.
[4]> # Generated from session /Users/njr/miro/log/2015/11/25/session256.miros
[5]> declare (>= (min Z) 1)
[6]> declare (<= (max Z) 92)
Miro Warning: Declaration failed: (<= (max Z) 92)
[7]> declare (= (countnull Z) 0)
[8]> declare (non-nulls-unique Z)
[9]> declare (>= (min (length Name)) 3)
[10]> declare (<= (min (length Name)) 12)
[11]> declare (= (countnull Name) 0)
[12]> declare (non-nulls-unique Name)
[13]> declare (>= (min (length Symbol)) 1)
[14]> declare (<= (min (length Symbol)) 2)
[15]> declare (= (countnull Symbol) 0)
[16]> declare (non-nulls-unique Symbol)
[17]> declare (>= (min Period) 1)
[18]> declare (<= (max Period) 7)
[19]> declare (= (countnull Period) 0)
[20]> declare (>= (min Group) 1)
[21]> declare (<= (max Group) 18)
[22]> declare (>= (min (length ChemicalSeries)) 7)
[23]> declare (<= (min (length ChemicalSeries)) 20)
[24]> declare (= (countnull ChemicalSeries) 0)
[25]> declare (= (countzero
(or (isnull ChemicalSeries)
(in ChemicalSeries (list "Actinoid" "Alkali metal"
"Alkaline earth metal"
"Halogen" "Lanthanoid"
"Metalloid" "Noble gas"
"Nonmetal" "Poor metal"
"Transition metal"))))
0)
[26]> declare (>= (min AtomicWeight) 1.007946)
[27]> declare (<= (max AtomicWeight) 238.028914)
Miro Warning: Declaration failed: (<= (max AtomicWeight) 238.028914)
[28]> declare (= (countnull AtomicWeight) 0)
Miro Warning: Declaration failed: (= (countnull AtomicWeight) 0)
[29]> declare (> (min AtomicWeight) 0)
[30]> declare (>= (min (length Etymology)) 4)
[31]> declare (<= (min (length Etymology)) 39)
[32]> declare (= (countnull Etymology) 0)
Miro Warning: Declaration failed: (= (countnull Etymology) 0)
[33]> declare (>= (min RelativeAtomicMass) 1.007946)
[34]> declare (<= (max RelativeAtomicMass) 238.028914)
Miro Warning: Declaration failed: (<= (max RelativeAtomicMass) 238.028914)
[35]> declare (= (countnull RelativeAtomicMass) 0)
Miro Warning: Declaration failed: (= (countnull RelativeAtomicMass) 0)
[36]> declare (> (min RelativeAtomicMass) 0)
[37]> declare (>= (min MeltingPointC) -258.975000)
[38]> declare (<= (max MeltingPointC) 3675.0)
[39]> declare (>= (min MeltingPointKelvin) 14.200000)
[40]> declare (<= (max MeltingPointKelvin) 3948.0)
[41]> declare (> (min MeltingPointKelvin) 0)
[42]> declare (>= (min BoilingPointC) -268.930000)
[43]> declare (<= (max BoilingPointC) 5596.0)
[44]> declare (= (countnull BoilingPointC) 0)
Miro Warning: Declaration failed: (= (countnull BoilingPointC) 0)
[45]> declare (>= (min BoilingPointF) -452.070000)
[46]> declare (<= (max BoilingPointF) 10105.0)
[47]> declare (= (countnull BoilingPointF) 0)
Miro Warning: Declaration failed: (= (countnull BoilingPointF) 0)
[48]> declare (>= (min Density) 0.000089)
[49]> declare (<= (max Density) 22.610001)
Miro Warning: Declaration failed: (<= (max Density) 22.610001)
[50]> declare (= (countnull Density) 0)
Miro Warning: Declaration failed: (= (countnull Density) 0)
[51]> declare (> (min Density) 0)
[52]> declare (>= (min (length Description)) 1)
[53]> declare (<= (min (length Description)) 83)
[54]> declare (>= (min (length Colour)) 4)
[55]> declare (<= (min (length Colour)) 80)
10 warnings and 0 errors generated.
Job completed after a total of 10.2801 seconds.
Logs closed at 2015/11/25 17:08:23 host tdda.local.
Logs written to /Users/njr/miro/log/2015/11/25/session259.
By default, Miró generates warnings when declared constraints are violated.
In this case, ten of the declared constraints were not met,
so there were ten warnings. We can also set the declarations to generate
errors rather than warnings, allowing us to stop execution of a script
if the data fails to meet our declared expectations.
In this case, the failed declarations are mostly unsurprising and
untroubling. The maximum values for Z, AtomicWeight,
RelativeAtomicMass, and Density all increase in this version of the
data, which is expected given that all the new elements are heavier
than those in the initial analysis set. Equally, while the fields
AtomicWeight, RelativeAtomicMass, Etymology, BoilingPointC,
BoilingPointF and Density were all populated in the original dataset,
each now contains nulls. Again, this is unsurprising in this case,
but in other contexts, detecting these sorts of changes in a feed of
data might be important. Specifically, we should always be interested
in unexpected differences between the datasets used to
develop an analytical process, and ones for which that process is used
at a later time: it is very possible that they will not be handled
correctly if they were not seen or considered when the process was
developed.
There are many further improvements we could make to the current state
of the autoconstraint generation, and there are other kinds of
constraints it can generate that we will discuss in later posts. But
as simple as it is, this level of checking has already identified a
number of problems in the work we have been carrying out with
Skyscanner and other clients.
We will return to this topic, including discussing how we might
add tool support for revising constraint sets in the light of failures,
merging different sets of constraints and adding constraints that are
true only of subsets of the data.
Parting thoughts
Outputs and Intermediates.
While developing the ideas about automatically generating constraints,
our focus was mostly on input datasets. But in fact, most of the ideas
are almost as applicable to intermediate results and outputs (which,
after all, often form the inputs to the next stage of an analysis pipeline).
We haven't performed any analysis in this post, but if we had, there might
be similar value in generating constraints for the outputs as well.
Living Constraints and Type Systems.
In this article, we've also focused on checking constraints at
particular points in the process—after loading data, or after
generating results. But it's not too much of a stretch to think of
constraints as statements that should always be true of data, even as
we append records, redefine fields etc. We might call these living
or perpetual constraints. If we do this, individual field
constraints become more like types. This idea, together with dimensional
analysis, will be discussed in future posts.
